

īecause the back-side reflection for an uncoated sphere is imperfect, it is fairly common to add a metallic coating to the back half of retroreflective spheres to increase the reflectance, but this implies that the retroreflection only works when the sphere is oriented in a particular direction.Īn alternative form of the cat's eye retroreflector uses a normal lens focused onto a curved mirror rather than a transparent sphere, though this type is much more limited in the range of incident angles that it retroreflects. Practically, this can be approximated by a concentric sphere system. The spherical aberration problem with the spherical cat's eye can be solved in various ways, one being a spherically symmetrical index gradient within the sphere, such as in the Luneburg lens design. Commercial retroreflective beads thus vary in index from around 1.5 (common forms of glass) up to around 1.9 (commonly barium titanate glass).

Finally, high index materials have higher Fresnel reflection coefficients, so the efficiency of coupling of the light from the ambient into the sphere decreases as the index becomes higher. Due to spherical aberration, there also exists a radius from the centerline at which incident rays are focused at the center of the rear surface of the sphere. For one, it is sometimes preferable to have an imperfect, slightly divergent retroreflection, as in the case of road signs, where the illumination and observation angles are different. In practice, the optimal index of refraction may be lower than n i + 1 ≅ 2 due to several factors. In that case, the sphere surface behaves as a concave spherical mirror with the required curvature for retroreflection.
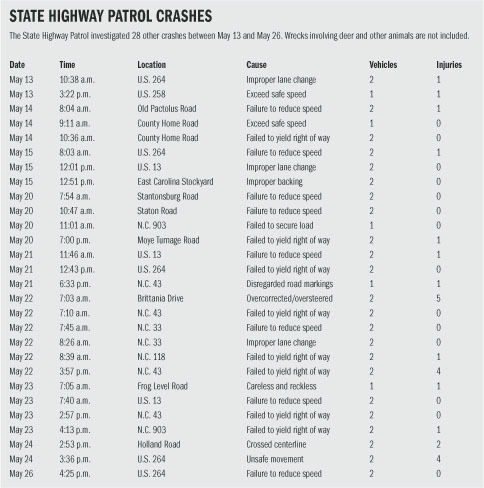
#REFLECTOR 2 CRASHES PLUS#
In the paraxial approximation, this effect can be achieved with lowest divergence with a single transparent sphere when the refractive index of the material is exactly one plus the refractive index n i of the medium from which the radiation is incident (n i is around 1 for air). These two types have similar optical properties.Ī large relatively thin retroreflector can be formed by combining many small corner reflectors, using the standard hexagonal tiling.Īnother common type of retroreflector consists of refracting optical elements with a reflective surface, arranged so that the focal surface of the refractive element coincides with the reflective surface, typically a transparent sphere and (optionally) a spherical mirror. The second form uses mutually perpendicular flat mirrors bracketing an air space.
In this structure, the reflection is achieved either by total internal reflection or silvering of the outer cube surfaces. In the more common form, the corner is literally the truncated corner of a cube of transparent material such as conventional optical glass. Therefore, as the ray reflects first from side x then side y and finally from side z the ray direction goes from to to to and it leaves the corner with all three components of its direction exactly reversed.Ĭorner reflectors occur in two varieties. When the ray reflects from the first side, say x, the ray's x-component, a, is reversed to − a, while the y- and z-components are unchanged. The three corresponding normal vectors of the corner's sides form a basis ( x, y, z) in which to represent the direction of an arbitrary incoming ray. A set of three mutually perpendicular reflective surfaces, placed to form the internal corner of a cube, work as a retroreflector.


 0 kommentar(er)
0 kommentar(er)
